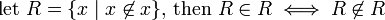As Guillermo Martinez said rightly in one of his essays, “it’s well-known that there is only one more effective way to kill conversation in a waiting room than to open a book, and that is to open a book of mathematics”. Still you may read more than this first sentence!
Even in high tech. innovation and entrepreneurship, the topic of imagination vs. reason, which could be translated by technology push vs. market push, is recurrent. So when I read books about creativity, whether it is scientific or artistic, I am always looking for links with innovation. I had the opportunity to check it again with Guillermo Martinez’s Borges and Mathematics. Borges is probably one of the “poets” who put the most mathematics in his literary work. Guillermo Martinez who is both a novel author and a mathematician has recently published in English this nice little book about Mathematics in Borges’ short stories. I already talked about mathematics in a recent post so let me add here a few things about what I liked.

Martinez quotes Borges who quotes Poe: “I – naively perhaps – believe Poe’s explanations. I think that the mental process he adduces corresponds to the actual creative process. I’m sure this is how intelligence works: through changes of mind, obstacles, elimination. The complexity of the operation he describes doesn’t bother me; I suspect that the real approach must have been even more complex and much more chaotic and hesitant. All this does not mean to suggest that the arcana of poetic creation were revealed by Poe. In the links, that the writer explores, the conclusion he draws from each premise is logical of course but not the only one necessary.” Borges in The genesis of Poe’s “The Raven”.
And then he adds more about the process of creativity: In the discussion of “divine, winged” intuition versus the prosaic, tortoise pace of logic, I would like to contradict a myth about mathematics: the process Borges describes is exactly the same as what happens in mathematical creation. Let’s consider the mathematician who has to prove a theorem for the first time. Our mathematician sets out to prove a result without even knowing if such a proof really exists. He gropes his way through an unknown world, proving and making mistakes, refining his hypothesis, starting all over again and trying another approach. He too has infinite possibilities within his grasp and with every step he takes. And so each attempt will be logical, but by no means the only one possible. It is like the moves of a chess player. Each of the chess player’s moves conforms to the logic of the game in order to entrap his rival, but none is predetermined. This is the critical step in artistic and mathematical elaboration, and in any imaginative task. I don’t believe there is anything unique to literary creation as far as the duality of imagination/intuition versus logic/reason is concerned.
I strongly believe that innovation is very similar to the process of artistic or scientific creation. But in another essay, Martinez says more about creation: “It’s the same feeling of euphoria you get when, after many years of struggling with your own ignorance, you suddenly understand how to look at something. Everything becomes more beautiful, and you have the feeling you can see farther than before. It’s a glorious moment, but you pay a great price for it, which is your obsession with the problem, like a constant wound or a pebble in your shoe. I wouldn’t recommend that sort of life to anyone. Einstein had a close friend, Michele Besso, with whom he discussed many details of the theory of relativity. But Besso himself never accomplished anything important in science. His wife once asked Einstein why, if in fact her husband was so gifted. “Because he’s a good person!” Einstein replied. And I think it’s true. You have to be a fanatic, and that ruins your life and the lives who are close to you.” Again you might meditate about the high rate of divorce in Silicon Valley and the fanatism creativity requires.
For those really interested in mathematics, I cannot avoid mentioning some other topics Martinez addresses: Gödel’s incompleteness theorem is one of the greatest achievements in mathematics ever, though it is complicated to understand. In a very simplistic ways, even in mathematics, there are things which are true but cannot be proven. Russell’s paradox is nearly as mesmerizing but simple to grab: (From Wikipedia): There are some versions of this paradox that are closer to real-life situations and may be easier to understand for non-logicians. For example, the Barber paradox supposes a barber who shaves all men who do not shave themselves and only men who do not shave themselves. When one thinks about whether the barber should shave himself or not, the paradox begins to emerge. According to naive set theory, any definable collection is a set. Let R be the set of all sets that are not members of themselves. If R qualifies as a member of itself, it would contradict its own definition as a set containing all sets that are not members of themselves. On the other hand, if such a set is not a member of itself, it would qualify as a member of itself by the same definition. This contradiction is Russell’s paradox. Symbolically: